
As students and teachers have traversed the educational landscape throughout the last year, two things are very certain. The first, is that teachers, schools, and districts have had to adapt their systems and structures of instruction to meet the needs of their students. The second, is that as a result of that adaptation, great teaching and learning has taken place.
Even in a normal school year, learning loss takes place in multiple content areas due to the summer break, extended periods of inclement weather, sickness, the list goes on and on. But recently due to the pandemic, loss of adequate instructional time and sometimes even resources have caused a larger gap in proficiency than normal.
 During my tenure as a district administrator, my team and I worked extremely hard in planning for summer camps as early as January to make sure that students entered their next grade level at the same level of proficiency when they exited their previous grade level. In this article, I want to share a few systems and structures that can help curve the learning loss in mathematics due to the recent pandemic.
During my tenure as a district administrator, my team and I worked extremely hard in planning for summer camps as early as January to make sure that students entered their next grade level at the same level of proficiency when they exited their previous grade level. In this article, I want to share a few systems and structures that can help curve the learning loss in mathematics due to the recent pandemic.
As school or district administrators, you have a very important role to play in your students' success. Resources, materials, professional development, school schedule, and even format of a block of instructional time are all things considered when making decisions year after year.
Here are a few systems and structures that can help you with the decisions you will be making in regards to mathematics instruction.
Four-Step Problem Solving Model
One of the most impactful and beneficial systems you can implement within a grade-level, entire school, or district is a consistent four-step problem solving model. This prevents acronyms from being utilized that can have negative effects on student proficiency during the year and on standardized tests. The concept of a problem-solving model is a pretty simple one. Basically, how your teachers teach students to approach a math problem.
Step 1: Understand the problem.
It begins with teaching young learners to understand a problem first. This is not the same as teaching students to locate key words to help them identify whether they need to add, subtract, multiply, or divide. As a matter of fact, that can cause students to get the incorrect answer and the majority of the time, that wrong answer is a choice on a standardized test.
Teach students how to visualize what the problem is asking through role play, acting, or even drawing. I still use this method today.
 Step 2: Apply Strategies.
Step 2: Apply Strategies.
Once a student really understands what the problem is asking, then have teachers choose from a variety of strategies to have students choose which ones work for them, as they begin to solve the problem. Some of these strategies include…
- Using manipulatives
- CCW (Count, Compute, Write)
- Draw a picture or diagram
- Generalize a pattern
- Guess & Check
- Organize Information
- Simplify the problem
- Use Logical Reasoning
- Work Backwards

Look at the example below and read the dialogue between two students that know what the problem is asking and how they go about using the Guess & Check strategy to figure out the answer.
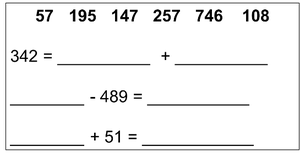
Nick and Lauren are working together. They have read the problem and
understand that they are to write the numbers so that the equations are true.
Lauren sighs and says, “We’ll never get this. There are too many choices.”
Nick responds, “I agree, but maybe we could try something. Let’s just write
the numbers and see what happens.” Lauren agrees and proceeds to fill in
the numbers randomly. As she does so, she says, “Wait, 746 can’t go here; the
whole thing is only 342.” She continues, “And it can’t be added to 51 either
because it is the biggest number.” Nick then builds on her thinking, “So it has
to go before 489. We are totally getting this.”
By making a guess and checking it, Nick and Lauren came to understand necessary relationships among the numbers they chose and the other numbers in the equation.
Step 3: Justify Your Thinking.
The third portion of this problem-solving model can be to have your teachers teach students to communicate and justify their thinking. It is essential that we ask students to communicate their thinking and coincidentally enough, part of our standards. This achievable regardless of the type of instruction that is taking place: remote, online, in-person, or hybrid.
Here is another example of what this looks like and why it is important to follow-up with questions that force students to justify their thinking.
Philip and Rosa are skiing down a ski trail.
Philip is 2/6 of the way down the trail.
Rosa is 2/8 of the way down the trail.
Who is farther down the trail?

This student is correct however, how do we know that this student understands fully how to compare fractions? Consider this follow-up question: What if Rosa was 4/8 of the way down the hill?
The student response to the follow-up question is a true testament to their understanding and also gives access to new mathematical ideas.
 Step 4: Facilitate Discourse.
Step 4: Facilitate Discourse.
The last component of a problem-solving model can take place at the beginning of every math lesson in your school. Daily Math Activities or Math Warm-Ups are proven to be successful in activating a student thinking process and making them ready for the lesson ahead.
Here is a summary of what to think about when planning these activities:
- Very brief
- Requires collaborative or independent completion
- How to think like a mathematician
- Make connections to themselves, others, or content areas
- Clarify understanding of vocabulary
- Repeated opportunities to revisit important mathematical BIG IDEAS
Here is an example of what this activity can look like in a small amount of instructional time.


Imagine the conversations that can take place in groups of students or even as a whole group discussion topic. Here are some of the discussion questions that I ask towards the end of this activity in order of the highest amount of teacher support to the lowest amount of teacher support:
 | Look carefully at the chart we created. Are there any representations that you wonder about? Why do you wonder about that representation? |
 | Why do you think it is important to be able to represent numbers in different ways? |
 | What math reasoning did you use to determine that your representation is equal to the number on your chart? |
 | How does understanding whole numbers, fractions, decimals, and percentages help you represent numbers in different ways? |
 | When would we want to find other representations of a number? |

About The Author
About Alan Becker, Academic Officer for Teacher Created Materials
Alan Becker specializes in best practices for curriculum and instruction. He provides professional development and training in the content areas of math, ELA, and social studies using TCM curriculum materials and Shell Education professional resources for school districts, teachers, and educational trainers. Prior to his work as an Academic Officer, Mr. Becker served as a District Elementary Education Specialist with Pitt County Schools in Greenville, North Carolina.
Strategies for Reversing Learning Loss in Mathematics in 2021